In the last post we used the Python tkinter module (which is standard) to build a shell window for script-based calculator app. To do anything useful, the shell needs a back-end calculator object to implement script parsing and executing functions.

In this post we’ll look at code for a script-driven prefix calculator that can be easily extended to include other (mathematical) functions.

As discussed last time, a valid math function — one that can be evaluated to produce a result — has a tree structure comprised of three types of nodes. Firstly, the operator nodes that represent the math operations. These nodes have zero or more child nodes (of any type) that are the inputs (value terms) for the operator.

As a simple example, the expression adding two and three (to get five) can be expressed in a variety of basic ways:

• Good old in-fix notation: 2 + 3
• Postfix (aka Reverse Polish) notation: 2 3 +
• Prefix (aka Polish) notation: + 2 3
• Functional notation: add(2, 3)
• Functional script notation: add 2 3

The word “Polish” above refers to the nationality of Jan Łukasiewicz (1878-1956), who invented prefix (“Polish”) notation in 1931. Note how prefix notation resembles how functions are called. More importantly, note how — so long as all functions have a fixed number of parameters (zero to N) — we can drop the functional parentheses for a simple script notation.

Both postfix and prefix notation are notable for not requiring parentheses to disambiguate compound expressions. Only infix suffers from ambiguity that must be resolved with order of operation rules (e.g. add and subtract before multiplying or dividing).

Consider a compound expression like:

a + b * c

Should it be (a+b)*c or a+(b*c)? The rules of precedence usually require addition before multiplication, so — though looking ambiguous — most will interpret it as (a+b)*c. But this requires agreed precedence rules and remembering those rules.

Consider the same expression in either prefix or postfix notation:

a b + c *
* + a b c

a b c * +
+ a * b c

The first two lines show (a+b)*c; the last two lines show a+(b*c). No parentheses required because there is no ambiguity in the expressions.

Many (including myself) have a soft spot for RPN (largely due to having used HP calculators that implemented it). I started this project using RPN but found it unwieldy. Setting a variable especially so because the semantics aren’t clear to me:

42 varname set

Or:

varname 42 set

I found I could make a case either way. The first implies “given value 42 bind it to varname” — a rightwards movement of data (which is more consistent with postfix notation). The second implies “given varname, bind it to value 42″ — a leftwards movement, the usual assignment flow.

It put ambiguity back into an otherwise unambiguous syntax. Just as precedence rules require remembering, so do the order of terms in the set operation. D’oh!

I couldn’t decide which looked best and was pretty sure I’d keep forgetting, so I bailed on postfix and switched prefix. Here the order seems more obvious:

set varname 42

One could put the value first and imply a rightwards movement, but nearly every programming language uses leftwards movement for assignment, taking the right-hand value and binding it to the left-hand name.

Name-first also seems more reasonable in a function call — Python’s built-in setattr function being an example:

setattr(object, name, value)

So, set varname value it is. Much easier to remember, too, I think.

Going back to the ambiguous expression above, the script notation for (a+b)*c:

mul add a b c

The tree structure is inherent and can be made apparent with indentation:

mul
    add
        a
        b
    c

This functional script prefix notation is what our calculator implements.

If we scan the code from last time looking for occurrences of self.calc and massage the results to eliminate duplicates and reduce it to its basics, we get something like this:

self.calc = Calculator()

tokens = self.calc.parse_text(text)
answer = self.calc.execute(tokens)
self.calc.reset()
self.calc.results
self.calc.variables.items()
self.calc.opnames()

This is the interface our calculator must implement. Firstly, we need a class named Calculator. The first two methods listed, parse_text and execute, seem self-explanatory. The former takes some text and returns tokens; the latter takes those tokens and returns an answer. The reset method seems obvious, too; it resets the calculator.

The results property is a list used by the F1 View Results menu selection. The variables property is a dictionary (note the items method) that returns name/value pairs (for the F2 View Variables menu selection). The opnames method returns a list of operator names (for the F4 View Operators menu selection).

We’ll implement these and a bit more.

The parse_text and execute methods indicate the calculator works in two stages, a lexical compile stage and a run-time execute stage. The former’s output, a list of tokens, is the latter’s input. The work each stage does depends on the language complexity and syntax. Our mathematical expression language is simple enough that neither stage is complicated.

The tokens are central, so let’s start there:

The Token class is a base class. The tokens returned by parse_text and operated on by execute will be one of the derived classes, DatumToken (a numeric value), NamedValToken (a variable or constant reference), or OperatorToken (a math operation to perform using values from the first two token types).

Here’s the DOC text for the class (left out of the code above for clarity):

Token class.

Implements a basic type/value token. A token instance is one of
three types: Constant, NamedVal or Operator. In a Constant, the
value is a literal (numeric) value. In a NamedVal, the value is
the name of a Variable. In an Operator, the value is the name
of the operator.

Class Attributes:
    Constant            a token type
    NamedVal            a token type
    Operator            a token type
    TTNames             list of token type strings

Instance Attributes:
    _t                  token type (internal)
    _v                  token value (internal)

Instance Properties:
    ttype               token type (use instead of _t)
    value               token value (use instead of _v)

Methods:
    (none)

A token is just a combined token-type and value. Note that NamedVal includes the constant names available for expressions (e.g. “pi” or “e”) because these are named values.

The run-time engine looks for names in the constants dictionary first. If the name is not found, it checks the variables dictionary. (If it doesn’t find it there, it raises an Exception.)

This means variables with the same name as a constant effectively vanish. The set command creates (or updates) one in the variables dictionary, but no other command can see it — they’ll always see the constant. (One improvement that could be made is having the set command complain about creating a variable with the same name as a constant.)

Now, at long last, we can look at the Calculator class, starting with its DOC text:

Prefix Calculator class.

Implements a script-based pre-fix math calculator.

Attributes:
    tokens              list of tokens to process
    variables           dictionary of variables
    constants           dictionary of constants
    result              list of outputs

Methods:
    reset               reset calculator
    execute             execute tokens
    <operator>          methods implementing each operator
    _get_value          get next value; evaluates operators

Class Methods:
    opnames             return list of operator names
    isoperator          determines whether a name is an operator
    datum               given a word, return an appropriate token
    parse_words         given list of words, return list of tokens
    parse_text          given text, return list of tokens

The class implements all the necessary attributes and methods listed above and a few more. The single leading underscore of the _get_value method marks it as a “private” method only the class should use. The five class methods should be fairly self-explanatory. We’ll look at their code below.

The intriguing one is the <operator> method. The <operator> is a fill-in for as many calculator operations as we care to implement. At minimum, we’d want add, sub, mul, and div, but, as you’ll see, the class is designed to make it almost trivial to add others.

As with last week’s Application class, the Calculator class is long, so I’ll break this one into chunks, too (the whole code is in the ZIP file). I won’t show the entire class in the post. There’s no point in listing operator after operator once it’s clear how it’s done.

Here’s the first chunk:

The SkipNames list (lines #9 to #14) contains method names that are not operators. The purpose of this list will be apparent below in the isoperator class method.

The initialization method (lines #16 to #27) creates the tokens and results lists as well as the variables and constants dictionaries. It populates constants with a variety of “built-in” constants that can be used in calculator source code. Note that both tokens and variables can be pre-populated with passed arguments.

The dunder repr method (lines #29 to #31) is standard for classes I design. The dunder str method (lines #33 to #35) returns the current tokens list as a string.

Next, two central class methods:

The isoperator class method (lines #42 to #57) takes a name and determines whether that name is an operator (i.e. a valid instance method that can be called to perform an operation on tokens). It explicitly excludes names beginning with an underbar, as well as methods beginning with “parse” (to exclude parse_text and parse_words). It also excludes names found in the SkipNames list.

Lastly, having filtered method names that are not operator methods, it sees if the name is an attribute of the class and returns True if so (else False).

The opnames class method (lines #37 to #40) starts with all the names in its class dictionary and filters them with isoperator to return a list of valid operator names.

Jumping ahead a little, we can exercise this method to see a list of operators:

When run, this prints:

60 items:
['acos', 'add', 'arccos', 'arcsin', 'arctan', 'asin', 'atan', 'atan2',
'avg', 'cbrt', 'ceil', 'ceiling', 'cos', 'cube', 'cuberoot', 'degs',
'div', 'divide', 'exp', 'fac', 'factorial', 'floor', 'hypot2', 'hypot3',
'inv', 'inverse', 'kg2lb', 'km2mi', 'lb2kg', 'ln', 'log', 'log10', 'log2',
'max', 'mi2km', 'min', 'mph2mps', 'mps2mph', 'mul', 'mult', 'multiply',
'now', 'plus', 'pow', 'power', 'pwr', 'rads', 'randnum', 'round', 'set',
'sin', 'sqr', 'sqrt', 'square', 'squareroot', 'sub', 'subtract', 'sum',
'tan', 'trunc']

The count of 60 is deceptive because it includes the aliases. Regardless, the above are all the operators available for calculator scripts.

The other three Calculator class methods deal with converting text to tokens:

The meat is in the datum method (lines #59 to #81). It takes a word and returns an appropriate Token types for (and containing) that word.

It first uses isoperator to see if the word is an operator. If so, it returns an OperatorToken. Next it tries converting the word to an integer. If this succeeds, it returns a DatumToken with the integer value. If it fails, it tries again, this time converting to a float. If that fails, the word has to be a (hopefully valid) reference to a constant or variable, so it returns a NamedValToken.

The parse_words class method (lines #83 to #85) expects a list of words that it passes through datum to convert to a list of Tokens. This method wasn’t required by the Calculator but is exposed here because parse_text needed it anyway.

The parse_text class method (lines #87 to #90) expects a string that it splits on whitespace into a list of words that it passes to parse_words (which converts the words to Tokens).

Let’s jump ahead again and exercise the parser:

When run, this prints:

Oper: set
Name: x
Oper: rads
Cons: 45
Oper: set
Name: y
Oper: rads
Cons: 45
Oper: sqrt
Oper: add
Oper: sqr
Oper: cos
Name: x
Oper: sqr
Oper: sin
Name: y

This is an example of a list of tokens the calculator processes to generate a result. In this case it will generate three. The two set operators each generate a result, and the equation:

Also generates a result — the last result, so the one the calculator returns as the result.

Getting back to the instance methods:

The reset method (lines #92 to #95) overwrites the variables dictionary and results list attributes with new empty ones (presumably pending a new calculation).

The execute method (lines # to #) processes tokens and populates results. It takes (and when used as a backend in our Application, expects) a list of tokens. In general use, if tokens are supplied at instance creation, they don’t need to be passed here. Either way, if execute receives an empty list, or finds tokens empty, it returns a “<null>” result (lines #105 to #108).

The execution engine itself is dead simple: So long as there are tokens to process, get a token value and append it to results. When the tokens are gone, use the last result as the return value. That’s all there is to it.

The _get_value method is an internal method used by the calculator to get the next available token value. It starts by popping the next token off the tokens list and then dispatching based on token type.

For DatumTokens, it returns the token’s value. For NamedValTokens, it looks up the name in constants, failing that variables, and returns the looked-up value (or raises ValueError if the name isn’t found). For OperatorTokens, it checks to be sure the name is valid (lines #146 and #147). If so, it gets the method (line #148) and invokes the operation (line #149). Note that it returns whatever value the operation returns.

If the token type is somehow none of these, it raises RuntimeException.

We can test this as we did the parser, but this time we’ll execute the list of tokens:

When run, this prints:

result = 1.0

calc-result: [0.7853981633974483, 0.7853981633974483, 1.0]

The first two results in the list are from the two set operations. The last one is the output.

That implements the calculator engine. All that remains are the methods that define each operation. We’ll start with a special one, the set method:

This is the most complicated one. It creates (or updates) a name in the variables dictionary. It starts by popping the next token off tokens and checking that it is a NamedValToken containing a name. Unlike the rest of the operator methods, we don’t use _get_value here because the token following set must be a name, it cannot be a literal value or operator (which _get_value would process for a return value).

Then, as with any binary operator, we use _get_value to get a value and put that in the named variable. (This, by the way, would be the place to check the constants dictionary and raise an Exception if the name exists there.)

All operations return a value, so we return the variable’s value.

This is the basic structure of all operations. Use _get_value to get however many operands are required, process them, and return a value. Many operations are binary and take two values, but there are also many unary operations that take one. There are even two that take none, and we’ll start with those:

The now operator (aka method) returns a float containing the number of seconds since midnight January 1, 1970 (as returned by the time.time function).

The randnum operator returns a float containing a random number, 0.0 <= N < 1.0 (as returned by the random.random function).

Note that these do not call _get_value and thus do not consume tokens. They only return a value. Note also that adding new operators is as simple as adding new methods named after the new operator.

Here are a few unary operators (selected from many):

Firstly, these (and all unary operators) first use _get_value to obtain the operator’s value. They return an appropriate value depending on the operation. Secondly, notice that we can define aliases for operators. User source code can use the name or alias interchangeably; there is no difference.

The code above defines the square, squareroot, log10, and log2 operators. It also defines sqr as an alias for square and sqrt as an alias for squareroot. The other unary operator methods all resemble these in form.

Here are some binary operators (and a three-operand one):

The pattern should be pretty obvious. These call _get_value twice to obtain the two operands they need and then perform their operation on them and return a value.

The log operator (unlike log10 or log2 above) takes a second parameter giving the log base. The hypot2 operator returns the Euclidean distance between two points in 2D space. The hypot3 operator does the same in 3D space. As you see, it requires three values.

Any other operators we define should work just like these. Just defining the method is all it takes to make the new operator part of the script language. Note that, since operators are implemented by methods with the same name, operator names have to be legal Python method names. This design doesn’t support operators like “+” or other symbols. (The underbar is a legal name character, so you could define an underbar operator.).

Finally, we can define some operators that work on lists. Because operators consume tokens according to their need, they must know how many operands are involved. This means any list operators must first have a count value, then the list items:

sum 5 21 42 63 84 106

This sums the five numbers 21, 42, 63, 84, and 106. These methods look like this:

They call _get_value to obtain the list length and then act on that many operands. Currently there is also a max and avg method to fill out the list operators group (see the code in the ZIP file for the full listing).

Now we have all the pieces for the calculator application:

When run, the calculator app window should appear:

Type a formula into the window and click the [Result] button (or press [F5]):

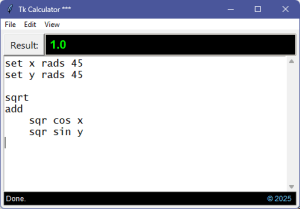
And now we’re done.

Enjoy your calculations and Merry Christmas (or other applicable holiday well wishes as appropriate)!

Next week I’ll post a short follow-up that turns our calculator into a word counter. As an illustration of how to create any other script-based processor you might like to implement.

Link: Zip file containing all code fragments from these two posts.

∅