In the previous post [see Elementary Cellular Automaton], I presented an implementation of a 1D elementary cellular automaton. Unfortunately, the code turned out to be an example of leaping into an idea without carefully reading the background information.

Long story short, while the code works and generates images, it doesn’t generate the correct images for all 256 rules. In this post, I present improved code that does.

I’m not here going to explain how cellular automata work. See the previous post for an explanation if needed. In this post, we’ll jump right into the problem with the first implementation and the changes that fix it.

To help get started (and because it’s needed by the code here), I will include the generate_rule function that gives us a rule dictionary given a rule number (an integer from 0 to 255, inclusive):

This is the same code from last time, so see the previous post for a detailed explanation. The short version is that the generate_rule function converts the integer to a list of the binary bits comprising the integer and builds a dictionary with three-bit keys indexing each bit.

As an aside, the design here uses three-bit string keys (like “000” or “011”), which requires the automaton to also generate three-bit string keys. An alternative design uses three-element tuple containing the raw 1 or 0 values — for instance, (0,0,0) or (0,1,1). Both techniques work. I went with string versions because I have a faint inherent mistrust of comparing tuples. This is just a mental twitch on my part; using tuples is not a problem and is arguably a cleaner approach (there are some cases where it can bite you, but those cases don’t apply here).

The error I made was making the initial row only long enough to contain the starting pattern of nonblank cells. In the default case, the initial row has just the one nonblank cell: [1]. To make life easier for the algorithm, I implemented the expand_row function to ensure three blank cells at the row start and end: [0,0,0,1,0,0,0].

From the beginning, I worried that the padding cells would introduce artifacts, because “000” is a valid triplet with a rule output. In the case of Rule 110, which was the use case I designed around, the output for “000” is 0, so no issue was apparent. It was only when I compared the outputs of all 256 rules to the examples shown in Wikipedia that I realized the code was broken. It turned out that my concern about artifacts was correct.

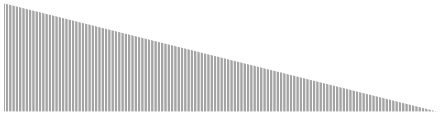
Any odd-numbered rule has output 1 for “000”, so using padding introduces artifacts for half the rules! In fact, Rule 1 outputs all zeros for all triplets except “000”. Which made the output for Rule 1:

Which is incorrect (by a long shot). The output for Rule 1 should look like this:

(Click on any of these images for a full-sized version.) Obviously, the padding thing was a Bad Idea. And the problem jumped out immediately upon comparing my outputs with the Wikipedia versions.

Further, after closely reading the Wikipedia page, although it isn’t explicit about this, it became apparent that the initial row — and all rows thereafter — need to be the same size. For one thing, if we want an initial row populated with something other than the default single centered nonblank cell, it’s much handier to have a full-length row to populate.

This immediately raises the question of how long the initial row needs to be. I decided that, because some patterns create a 45° slope from the default single nonblank cell, the initial row should be twice as long as the number of rows generated by the automaton. A good example is the output for Rule 126:

The final row is twice the length of the number of rows because the pattern grows in both directions from center at respective 45° angles.

We already have a size parameter controlling the number of rows to generate, so we’ll use two times its value to determine the row length (which, again, applies to all rows generated). We no longer want padding (because of the artifacts), so we can discard the expand_row function and replace it with the initial_row function:

The function begins (lines #5 and #6) by validating its inputs, size and start. Then it calculates how long the initial row needs to be (line #9). If the start parameter holds a list at least that long, we just return it (lines #12 and #13).

Otherwise, we calculate the padding necessary on each side to extend the list to the row length needed (line #16). The idea is that, if the start pattern is shorter than the row length, it will be centered in the row. Line #19 creates the initial row.

Finally (lines #21 to #24), we ensure the initial row is the correct length, because the round-off from the integer division in line #16 might leave it one cell short. I used a while loop to guarantee the final result is the correct length, but it should never be necessary to actually repeat the loop (assuming it happens even once).

Line #27 returns the created initial row. Note this is distinctly different from the expand_row function, which modified an existing row.

The code on lines #30 through #35 exercise the function.

With the generate_rule and initial_functions defined, we can move on to the run_automaton function:

This is essentially the same function as we used last time with only a handful of changes. The first change is that line #12 now calls the initial_row function rather than the expand_row function. Also, in line #46, we formerly passed the new row through the expand_row function to ensure padding, but now we can just assign new_row to row.

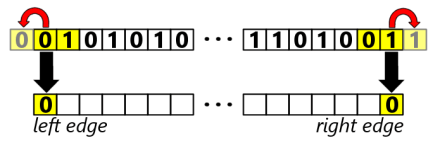
The bigger change involves lines #28 through #37. In the old version (because we knew there was always padding), we simply grabbed triplets to use as keys, which took only one line of code (line #32 in the old code). Now, because there is no padding and we want to put a rule output value into every cell of the new row, we need to compensate for two special cases where the triplet hangs off the edge of the row by one cell. (Remember, the center cell of the triplet is where the new value goes.)

Here’s an illustration of the requirement:

The faded cells in the above represent a “virtual” cell (that isn’t really there) on each end of the row. We duplicate the triplet center cell — whatever it is — as that virtual cell. Lines #29 to #31 handle the left-hand case, and lines #32 to #34 handle the right-hand case.

Other than these two changes, the code is the same as the old version. Lines #83 to #87 exercise the function.

For completeness — and to correct a minor bug from the old version — here again is the code that converts the generated row data into an image file:

There are a few minor changes. Firstly, lines#6 to #12 define some global constants the make_automata_bitmap function uses. The first two specify the background and foreground color (the old code had the constants in the code — a coding no-no).

The four NumberXxxx constants determine whether the output image has the rule number in the upper-left corner. They also specify the size, color, and font of the superimposed number. The code already allows for output files (both the text and image) to include the number in the filename. When enabled, the image looks like this:

Now the image self-identifies as Rule 30 (one of the more interesting rules besides Rule 110).

I wanted the image to include the rule number as part of the all-256-rules “catalog” image I created as a reference:

The catalog (click for big) shows all 256 rules, and the eight-column format highlights the commonality of rules. For instance, odd-numbered rules have darker backgrounds, largely because the output of a “000” triplet is a 1.

One thing I found interesting is the prevalence of Sierpiński triangles generated by a number of rules. Upon reflection, it makes sense given how this automaton works, but it surprised me at first (note the bigger version above from Rule 126).

And that’s about it for this time.

Link: Zip file containing all code fragments used in this post.

∅